http://www.saintpoint.org/Rappel de Mathématique, la Cotangente : Cercle trigonométrique sur un plan.
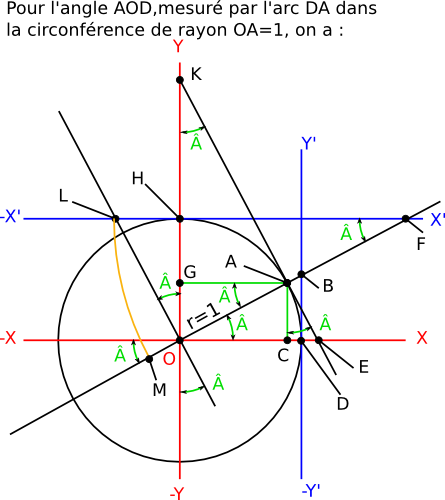
cotangente d'un triangle rectangle incrit dans le cercle trigonométrique (ici AOC)L'angle pris pour référence étant l'angle, noté Â, ayant son sommet en O, entre l'axe -XX et le droite OA (OA=hypothénuse de longueur 1) La cotangente d'un angle est le rapport du coté adjacent à l'angle diviser par le coté opposé de l'angle. Pour l'angle  on écrit cotg(Â) Pour le triangle AOC inscrit dans le cercle on a : cotg(Â)=OC÷CA et dans le triangle OAG : cotg(Â)=GA÷GO Mais ( si on y regarde bien, ) on retrouve aussi cotg(Â) : dans le triangle BOD : cotg(Â)=OD÷DB ; dans le triangle EOA : cotg(Â)=OA÷AE ; dans le triangle EAC : cotg(Â)=AC÷CE ; dans le triangle OFH : cotg(Â)=FH÷HO ; dans le triangle LOH : cotg(Â)=OH÷HL ; dans le triangle LFO : cotg(Â)=FO÷OL ; dans le triangle EKO : cotg(Â)=KO÷OE ; dans le triangle OKA : cotg(Â)=KA÷AO ; dans le triangle AKG : cotg(Â)=KG÷GA ; => ces rapports de longueur expriment tous la cotangente de l'angle Â. ; cotg(Â), est un coefficient de proportionnalité entre deux segments formant un angle Â, il n'a pas d'unité, ( ce qui veut aussi dire que le coté opposé à  et le coté adjacent de  ont la même unité de mesure ). => grace à Thalès, on peut dire si r = OD = OH = 1, que la cotangente de  représente la longueur HF = cotg(Â). La cotangente est une pente (distance÷hauteur) =cos(Â)÷sin(Â) =OC÷CA. C'est le paramètre "a" dans f(x)=ax+b de la droite KE. "a"=cotg(Â) =-(1÷tg(Â)) et : si (0<Â<=π/2)+(n×π) avec n=nombre entier, "b"=OA÷sin(Â) =1÷sin(Â) OU si (π/2<=Â<π)+(n×π) avec n=nombre entier, "b"=-OA÷sin(Â) =-1÷sin(Â) Pour sin(Â)=0 soit Â=0 ou Â=π ou Â=π+(N×π) (N étant un entier); cotg(Â)=1÷0 =∞(infini) donc la cotangente est verticale, (C'est la droite -Y'Y' ou sa symétrique r/r -YY) Pour cos(Â)=0 soit Â=π/2 ou Â=(π/2)+(N×π) (N étant un entier); cotg(Â)=0÷1 =0 donc la cotangente est horizontale, (C'est la droite -X'X' ou sa symétrique r/r -XX) Connaitre la cotangente de angle  et la longueur du coté opposé =sin(Â) d'un angle Â, permet de calculer maintenant, pour tous les angles  trouvés sur le dessin, la longueur du coté adjacent. Ou l'inverse connaissant le coté adjacent et la cotangente de l'angle  on calculera le coté opposé. Démonstration par l'exemple : La cotangente est, par définition, le coefficient qui divise par le sinus et mutiplie par le cosinus de l'angle. En divisant le coté opposé par le sinus de l'angle on trouve l'hypoténuse CA÷sin(Â) = rayon(OA) (voir § sinus). En multipliant le rayon par le cosinus de l'angle on trouve le coté adjacent OC =rayon(OA)×cos(Â) (voir § cosinus). La cotangente est le rapport cos(Â)÷sin(Â), multiplier le coté opposé par la cotangente réalise les deux opérations précédantes en une fois, donne le coté adjacent => CA×cotg(Â) =[CA÷sin(Â)]×cos(Â) =OA×cos(Â) =OC En pratiquePour faire une analogie concrète à la cotangente :Un rectangle OCAG a une diagonale OA(=GC)=1 ( pris comme unité ). Le coté adjacent OC=GA mesure 0.866, soit environ ((√3)/2)×diagonale OA. Le coté opposé CA = OG mesure 0.5 , soit 1/2 OA. La cotangente de  est par définition OC÷CA soit ((√3)/2)÷1/2=√3 (=environ 1,732050808) Pour info cet angle correspond à un arc de π/6 rd ( radian ) soit (180÷π)×(π÷6)=30°. APPLICATION RÉELLE exemple avec un toit : la hauteur d'un pan de toiture est de ( n×AC puisque OA=1), La longueur couverte sur une horizontale est de n×OC, l'inverse de la pente du toit est de (n×OC)÷(n×AC) =OC÷AC. Inconvénient, si on prend notre exemple n est un multiple de √3 ce qui n'est pas une unité de mesure bien pratique! C'est là qu'intervient Thalès et son théorème. Comme les droites GA et HF sont paralèlles, on peut affirmer que GA÷OG est ègale à HF÷OH avec OH=1 cette fois! cotg(Â) devient HF÷OH pour une longueur horizontale de 1. Notre hauteur de pan de toiture est de ( n'×OH avec OH=1), la longueur couverte sur une horizontale est de n'×HF, l'inverse de la pente du toit est de (n'×OH)÷(n'×HF) =OC÷CA. La longueur couverte par ce toit est directement connue en connaissant la hauteur de ce toit HF = n'(OH÷sin(Â)×cos(Â)) = n'(OH×cotg(â)). Comme OC÷CA est égale à OH÷HF la cotangente indique la longueur HF pour une longueur OH =1 (inverse de la pente sur un mètre) Application numérique : Remarque : 1/√3 =√3/3 comme on le voit aussi dans les tables mémo-techniques. => Si la hauteur du toit est de 5,77350269 mètres, soit 5,77350269×OH =(5×2)/√3)×OH (pourquoi ces nombres ? pour reprendre la démo § tangente), le rampant du toit est de 10×[OH÷sin(Â)] =10×OF =10×(1/√3)÷sin(Â) =10×(1/√3)÷1/2 =10×(2/√3), la longueur du plancher couvert par le toit est de =10×[OF×cos(Â)] =10×HF =10(2/√3)*cos(Â) =10×(2/√3)*(√3/2) =10×1 =10 mètres. La cotangente est bien l'inverse de la tangente. ou plus simplement : => 5,77350269×(cos(Â)÷sin(Â)) 5,77350269×cotg(Â). |