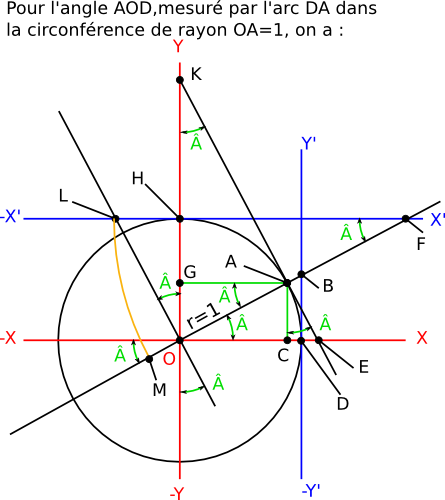
http://www.saintpoint.org/Rappel de Mathématique, le Cercle trigonométrique sur un plan.Conseil de lecture pour un novice ou une personne ayant beaucoup oublié. Expliquer les maths par du texte n'est pas simple, j'espère y parvenir tout de même à peu près ici. Lisez ce document une première fois paragraphe par paragraphe pour comprendre les explications. Ne vous arrêter pas sur les détails. Relisez le document en ne lisant que les textes en gras. Ces textes donnent les règles de la trigonométrie. Une fois que vous avez compris, relisez le documents en parcourant cette fois les exemples. Après ces étapes la trigonométrie ne devrait à nouveau plus avoir de secret pour vous!
Les termes en gras-souligné sont des règles trigonométriques. Je me répète, mais ce point est capital, le cercle trigonométrique ne fonctionne que dans un repère orthonormé. C'est à dire : 1) Les droites -XX et -YY qui se croisent en O sont perpendiculaires ( orthogonales ). 2) Les longueurs OD et OH, sont égales au rayon et de longueur 1. 3) Le cercle trigonométrique, passe donc par les points D, A, H, il a son centre en O, intersection des droites -XX et -YY. Rappel de ce qu'est un angle :Deux droites non parallèles forment un angle entre elles à leur point d'intersection. ex : OD et OA forme un angle  en O. L'angle  est aussi le rapport de la longueur de l'arc DA divisé par le rayon. Cet angle est alors exprimé en radian. L'angle en radian exprime le multiplicateur de la longueur du rayon OD pour obtenir la longueur l'arc DA. DA=Â×OD Un angle de un radian intercepte sur la circonférence du cercle centré sur cet angle, un arc de longueur égale au rayon de ce cercle.ex : OD et OH forment un angle de π/2 radian donc la longueur de l'arc DH = π/2 puisque rayon = 1. sur le graphique ci-dessus la longueur de l'arc est de : OD× si  est en radian, de OD×(Â×(180÷π)) si  est donné en degré, ( de OD×(Â×(200÷π)) si  est donné en grade ). Pour tracer un triangle ABC, avec un compas et un rapporteur, pour déterminer toutes les longueurs et tous les angles il faut connaitre : 1) soit trois longueurs de segments, partant des ces trois longueurs connues, vous pouvez tracer les trois angles inconnus du triangles, 2) soit un angle et deux longueurs, partant des ces deux longueurs et de cet angle connus, vous pouvez tracer les deux angles et la longueur inconnus du triangle, 3) soit deux angles et une longueur, partant des cette longueur et de ces deux angles connus, vous pouvez tracer l'angle et les longueurs inconnus du triangles, La trigonométrie utilise des termes qui ne sont en réalité que des règles de trois à appliquer. La trigonométrie défini une série de rapport de longueurs liés entre eux; sous des termes qui lui sont propre. Connaitre les termes trigonométriques et ce qu'ils représentent, permet de déterminer toutes les longueurs, tous les angles et arcs du dessin ci-dessus : 1) en connaissant seulement deux longueurs de segments d'un triangle, 2) ou en connaissant seulement un angle et une longueur d'un triangle, Pour la troisième fois dans cette page, mais encore exprimer autrement : Pour comprendre ces règles garder ceci en tête : la longueur OA est égale au rayon, la longueur est égale à 1. Tous les paramètres trigonométriques sont des rapports longueur/longueur ou rayon-angle. ( angle = longueur d'arc ÷ rayon ) Au moins un angle du triangle doit être droit ( formé par deux droites perpendiculaires ). La trigonométrie défini six rapports importants donc il faut connaitre au moins les quatre premiers, les termes utilisés pour définir ces rapports sont les suivants : - 1) sinus , - 2) cosinus , - 3) tangente , - 4) cotangente , - 5) sécante , - 6) cosécante. |