Formulaire technique libre et gratuit www.saintpoint.org, site de calcul en ligne.

Formulaire Technique A propos de l'auteur Menu | Dérouler tout | Fermer tout Navigation (Remonter) Page précédente. Chapitre précédant. Page principale du site. fermer Rappel cercle trigonométrique Cercle trigonométrique Sinus : Cercle trigo Cosinus : Cercle trigo Tangente : Cercle trigo Cotangente : Cercle trigo fermer

Datation de cette page
Date d'émission :
  le mardi 26 novembre 2024 à 20:53:29

Date de création :
  ( Année-Mois-Jour H:min:sec )
  le 2013-03-02 13:52:07
Date de la dernière mise à jour :
  le 2013-03-13 00:02:26

Nombre de visite de la page :
  compteur = 3836 vues.

Rappel de Mathématique, le Sinus : Cercle trigonométrique sur un plan.

Ci-contre le cercle trigonométrique sur un plan : Les termes en gras-souligné sont des règles trigonométriques. le cercle trigonométrique ne fonctionne que dans un repère orthonormé. C'est à dire :    1) Les droites -XX et -YY sont sur un plan ( espace euclidien ).    2) Les droites -XX et -YY qui se croisent en O sont perpendiculaires ( orthogonales ).    3) Les longueurs OD et OH, sont égales au rayon et de longueur 1.    4) Le cercle trigonométrique, passe donc par les points D, A, H, il a son centre en O, intersection des droites -XX et -YY.

Pour télécharger la page rappel mathématique Le sinus dans le cercle trigonométrique au format PDF, clic droit puis "Enregistrer la cible du lien sous ..."

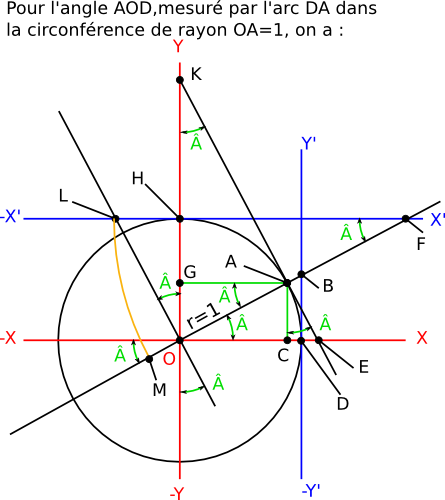
sinus d'un triangle rectangle incrit dans le cercle trigonométrique (ici AOC)

       L'angle pris pour référence étant l'angle, noté Â, ayant son sommet en O, entre l'axe -XX et le droite OA (OA=hypothénuse de longueur 1)

1) Le sinus d'un angle est le rapport du coté opposé à l'angle diviser par l'hypoténuse de l'angle ( = rayon pour les longueurs inscrites dans le cercle ). Pour l'angle  on écrit sin(Â)
Pour le triangle AOC inscrit dans le cercle on a : sin(Â)=CA÷r; =CA÷OA ; =CA÷OD ; =CA÷OH     et dans le triangle OAG : sin(Â)=OG÷r ;=OG÷OA ; =OG÷OD ; =OG÷OH

Mais ( si on y regarde bien, ) on retrouve aussi sin(Â) :
   dans le triangle BOD : sin(Â)=BD÷BO ;    dans le triangle EOA : sin(Â)=EA÷EO ;    dans le triangle EAC : sin(Â)=EC÷EA ;
   dans le triangle OFH : sin(Â)=OH÷OF ;    dans le triangle LOH : sin(Â)=LH÷LO ;    dans le triangle LFO : sin(Â)=LO÷LF ;
   dans le triangle EKO : sin(Â)=EO÷EK ;    dans le triangle OKA : sin(Â)=OA÷OK ;    dans le triangle AKG : sin(Â)=AG÷AK ;
    => ces rapports de longueur expriment tous le sinus de l'angle Â. ;

sin(Â), est un coefficient de proportionnalité entre deux segments formant un angle Â, il n'a pas d'unité, ( ce qui veut aussi dire que le rayon et le coté opposé à Â doivent avoir la même unité de mesure ).
   => on peut dire si rayon = OA = OD = OH = 1, que le sinus de  représente la longueur CA ( ou OG ) = sin(Â).

Le sinus d'un angle est la projection sur un axe parallèle au coté opposé, du rayon d'un cercle égale à l'hypoténuse. Cette projection se faisant suivant la direction du coté adjacent.
Ex 1 : Pour le triangle AOC, le sinus d'un angle  est la projection sur un axe parallèle au coté opposé AC, du rayon d'un cercle égale à l'hypoténuse OA. Cette projection se faisant suivant la direction du coté adjacent OC.
Ex 2 : Pour le triangle LFO, le sinus d'un angle  (=arc LM) est la projection sur un axe parallèle au coté opposé LO, du rayon d'un cercle égale à l'hypoténuse LF. Cette projection se faisant suivant la direction du coté adjacent FO.

Connaitre le sinus de angle  et la longueur de l'hypoténuse (=rayon du cercle) d'un angle Â, permet de calculer maintenant, pour tous les angles  trouvés sur le dessin, la longueur du coté opposé. Ou l'inverse connaissant le coté opposé et l'angle  on calculera l'hypoténuse.
Ex : la longueur OG = CA est égale = rayon(OA)×sin(Â) ou rayon(OA) = CA÷sin(Â) = OG÷sin(Â), etc...

En pratique

Pour faire une analogie concrète au sinus :
Un rectangle OCAG a une diagonale OA(=GC)=1 ( pris comme unité ). Le coté opposé AC=OG mesure 0,5, soit 1/2 diagonale OA.
    D'après Pythagore, OA=√(AC²+OC²) => OA=1=√((0,5)²+OC²) =√(0,25+OC²) => OC²=0,75. ( Puisque OA=1 )
    Donc OC²=0,75 => OC=√(3/4) = (√3)÷2 soit environ 0.866025404.

       Pour info cet angle correspond à un arc de π/6 rd ( radian ) soit (180÷π)×(π÷6)=30°.

Puisque AC est notre coté opposé à Â, AC est le sinus de l'angle Â, ce qu'on vérifie ici 0,5÷1 =0,5 = sin(Â) =longueur coté opposé r/r hypoténuse.

APPLICATION RÉELLE exemple avec un toit :
Un pan de toiture, de longueur ( n×OA puisque OA=1), est en pente par rapport à une l'horizontale, la hauteur du dénivelé de ce toit ( n×AC puisque OA=1 ) est de :
longueur du rampant du toit ( = projection verticale du toit =n×OA )× sin(angle du toit r/r horizontale) = n×(OA×sin(Â)) = n×AC.

Application numérique :
   => Si le rampant du toit a une longueur de 10 mètres ( 10×OA ), que l'angle du toit est  avec sin(Â)=0,5, la hauteur du dénivelé ( 10×CA ) est de 10×(OA×sin(Â)) = 10×0,5 =5 =10×AC.
    Vérification sin(Â)=[hauteur du dénivelé ( =coté opposé )]÷[longueur du rampant du toit ( =hypoténuse )] =5÷10 =0,5. Nous retrouvons bien notre sin(Â) !
   => On constate que les deux termes OA et OC ont le même multiplicateur, (n×OA)÷(n×OC)=OA÷OC. ce qui nous ramène bien au cercle trigonométrie OA =rayon =1

Pour connaitre l'angle  en radian il faut passer par :
    - l'équation du cercle (x²÷a²)+(y²÷b²)=1, soit pour le cercle trigonométrique (cos²(Â))+(sin²(Â))=1. Ce point sera expliquer dans un autre formulaire ( équation de l'ellipse ou du cercle = ellipse particulière ).
    - ou Pythagore OA²=OC²+AC². Puisque notre rayon est OA et qu'il est égale à 1=(cos²(Â))+(sin²(Â)). Tiens on trouve pareil dans les deux cas ! Ce point sera expliquer dans un autre formulaire Pythagore.
   Le plus simple est, ici, de lire la correspondance sin(Â) => Â dans une table, ou de le faire calculer par une calculatrice !

    - En pratique on a rarement besoin de connaitre l'angle qui oblige à utiliser un rapporteur d'angle. L'usage d'un compas et d'un moyen de mesure est plus précis en général, il est donc mieux de connaitre le sinus de cet angle.